- Text classification and Naive Bayes:
A rule captures a certain combination of keywords that indicates a class.
Hand-coded rules have good scaling properties, but creating and maintaining
them over time is labor intensive.
Our goal in text classification is high accuracy on test data or new data – for example, the newswire articles that we will encounter tomorrow morning in the multicore chip example. It is easy to achieve high accuracy on the training set (e.g., we can simply memorize the labels). But high accuracy on the training set in general does not mean that the classifier will work well on new data in an application. When we use the training set to learn a classifier for test data, we make the assumption that training data and test data are similar or from the same distribution.
The Bernoulli model:
Properties of Naive Bayes
Even when assuming conditional independence, we still have too many parameters for the multinomial model if we assume a different probability distribution for each position k in the document. The position of a term in
a document by itself does not carry information about the class. Although there is a difference between China sues France and France sues China, the occurrence of China in position 1 versus position 3 of the document is not useful in NB classification because we look at each term separately. The conditional independence assumption commits us to this way of processing the evidence.
Vetor Space Classification:
The document representation in Naive Bayes is a sequence of terms or a binary vector 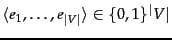 . In this chapter we adopt a different representation for text classification, the vector space model, developed . It represents each document as a vector with one real-valued component, usually a tf-idf weight, for each term. Thus, the document space
. In this chapter we adopt a different representation for text classification, the vector space model, developed . It represents each document as a vector with one real-valued component, usually a tf-idf weight, for each term. Thus, the document space 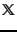 , the domain of the classification function
, the domain of the classification function 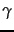 , is
, is 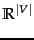 . This chapter introduces a number of classification methods that operate on real-valued vectors.
. This chapter introduces a number of classification methods that operate on real-valued vectors.
The basic hypothesis in using the vector space model for classification is the contiguity hypothesis .
Flat Clustering:
Clustering algorithms group a set of documents into subsets or clusters . The algorithms' goal is to create clusters that are coherent internally, but clearly different from each other. In other words, documents within a cluster should be as similar as possible; and documents in one cluster should be as dissimilar as possible from documents in other clusters.
Clustering is the most common form of unsupervised learning . No supervision means that there is no human expert who has assigned documents to classes. In clustering, it is the distribution and makeup of the data that will determine cluster membership.
The difference between clustering and classification may not seem great at first. After all, in both cases we have a partition of a set of documents into groups. But as we will see the two problems are fundamentally different. Classification is a form of supervised learning: our goal is to replicate a categorical distinction that a human supervisor imposes on the data. In unsupervised learning, of which clustering is the most important example, we have no such teacher to guide us.
The key input to a clustering algorithm is the distance measure, the distance measure is distance in the 2D plane. This measure suggests three different clusters in the figure. In document clustering, the distance measure is often also Euclidean distance. Different distance measures give rise to different clusterings. Thus, the distance measure is an important means by which we can influence the outcome of clustering.
Flat clustering creates a flat set of clusters without any explicit structure that would relate clusters to each other. Hierarchical clustering creates a hierarchy of clusters and will be covered.
Hierarchical clustering
hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two type:
- Agglomerative: This is a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: This is a "top down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In general, the merges and splits are determined in a greedy manner. The results of hierarchical clustering are usually presented in a dendrogram.
In the general case, the complexity of agglomerative clustering is  , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is  , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 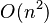 ) are known: SLINK[1] for single-linkage and CLINK[2] for complete-linkage clustering.
) are known: SLINK[1] for single-linkage and CLINK[2] for complete-linkage clustering.
 , which makes them too slow for large data sets. Divisive clustering with an exhaustive search is
, which makes them too slow for large data sets. Divisive clustering with an exhaustive search is  , which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity
, which is even worse. However, for some special cases, optimal efficient agglomerative methods (of complexity 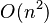 ) are known: SLINK[1] for single-linkage and CLINK[2] for complete-linkage clustering.
) are known: SLINK[1] for single-linkage and CLINK[2] for complete-linkage clustering.![\includegraphics[width=4cm]{visualclusters.eps}](http://nlp.stanford.edu/IR-book/html/htmledition/img1387.png)
没有评论:
发表评论